Background
Motivation
In machine learning, we often create models that are exceedingly complex, so much so that we cannot explain the function modelled by the algorithm. Deep neural networks are an example of this, as we usually don’t know how the model works, it just does. Another example can be decision trees, especially those with a large number of features or a great depth. We often refer to these models as black boxes.

When working with a black box, optimization can be difficult. Most of the optimizers we’re familiar with use differentiation in some form. Put simply, this involves taking a function, and then calculating the slope at a given point.
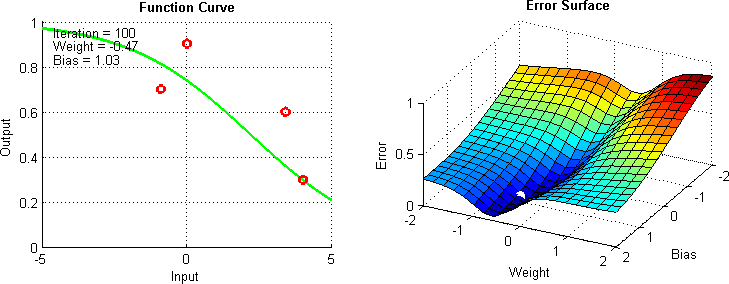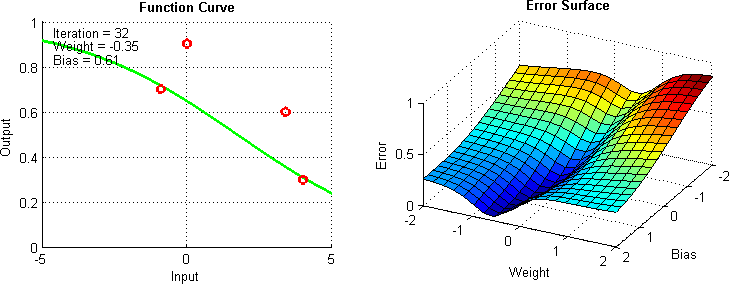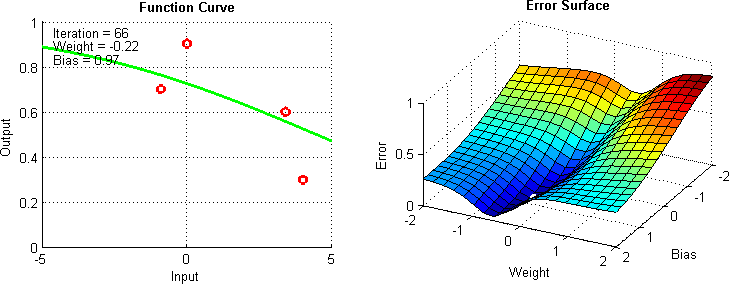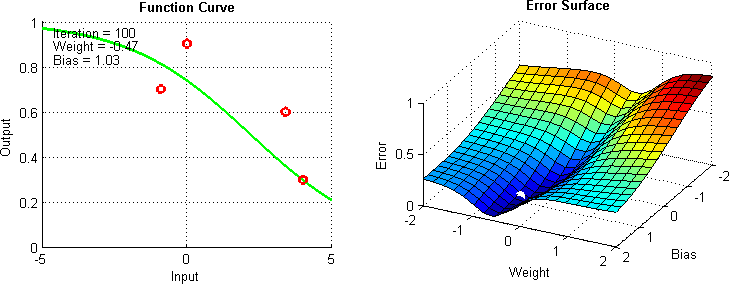
However, when working with a black box, taking a derivative can be a pain in the neck. For one, the functions might not be smooth, which is a necessary precondition for differentiation. Moreover, some models are just very complex, in which case differentiation could be computationally complex and just unreasonable.
Overview
This problem is the motivation for derivative-free optimization. These are optimizers which (suprise) don’t rely on differentiation. This a broad a category of algorithms and interested readers can check out this paper for an examination of the field. In this lecture, we will cover two such algorithms: Nelder-Mead and Genetic Algorithms.
Nelder-Mead
The Nelder-Mead optimzation algorithm is probably the most popular derivative free optimizer.
The algorithm utilizes a simplex, defined as the convex hull of $n+1$ vertices in $R^n$. For the 2-D plane, this is a triangle. For 3-D space, this is a tetrahedron. Today’s discussion will be limited to the triangle, but the algorithm can be generalized to $n$ dimentions.

The general idea of the algorithm is to “zero in” on the lowest value by transforming our triangle. Here are the usual steps:
- Select three points in the plane to construct a nondegenerate triangle.
- Determine the best, second-best, and worst vertices. Define the best side to be the side opposite to that of the worst vertex.
- Attempt to generate a third point with a lower value by expanding, contracting, and reflecting with respect to the best side. If two attempts fail, shrink the triangle towards the best side.
- Repeat steps 2 and 3 until a condition is met.
Here is what it looks like:

A Closer Look
What exactly do these reflections, expansions, and contractions look like? Let’s break it down step-by-step.
Let’s call the best point $x_l$, the second best $x_s$, and the worst $x_h$.
First, we directly reflect $x_h$ over the best side. We can do this by computing the centroid along the best side. Call this new point $x_r$.

Now, is $x_r$ the new best point? Is it better than $x_l$? If so, let’s try to expand further in that direction to further lower the value.

If that doesn’t work, then give up and accept $x_r$.
If $x_r$ is not the new best point, we now try to contract. Is $x_r$ better than the old point? Does it have a lower value than $x_h$? If so, we contract outside.

Was it worse? Then we contract inside.

Now, while it is rare, there is a chance that even contraction fails to reduce the value. In that case, we shrink instead.

Can We Stop Now?
There are a few ways to specify a satisfactory condition.
First, we can say that at some point, the simplex is small enough. Say, the points are close enough to one another, or the area of the triangle passes some threshold.
Or, we can specify that at some point, the values at each of the points are close enough. At some point, the improvement in value is so small that the difference between the points is very small.
Finally, we can specify beforehand that we will only conduct a certain, maximum number of iterations.
Genetic Algorithms
Genetic algorithms are a type of heuristic search algorithm within the domain of evolutionary algorithm.
As noted in its name, Genetic Algorithms use genes to describe a certain answer, and evolution to guide the genes to optimize a certain objective function, called the fitness function.
The process is typically as follows:
- We begin with a random or predetermined populaton
- Each member in the population, with a certain gene, is judged or ranked by a fitness function
- The fittest species will “survive” and move on to the breeding stage.
- The survivors crossover, or blend with each other, and certain random mutations are introduced.
- Repeat steps 2 - 4 until a condition is met
Now, lets take a look at an example:
2D Cart Genetic Algorithm Optimization
Where are my Genes?
Let start with some terminology.

The three main terms are gene, chromosome, and population.
A gene is a particular feature of our answer. Genes are the most basic feature in our program, no gene could be divided into smaller features.
Example of genes:
- Whether to include an object or not (boolean)
- The x coordinate of a wheel (float)
- How many wheels? (integer)
A chromosome fully describes one species. We are evaluating a species using a fitness function, we are really looking at how well the chromosome does. Our final answer is a chromosome that describes the fittest species.
The population is the set of all the species we are evaluating or alive. Only the best performing species will reach the next round of crossovers and mutations.
Crossovers and Mutations
Once the best performing species are selected, they will move the next round of breeding.
For each pair of the surviving species, they will first crossover, and then the resulting chromosomes will mutate.
Crossovers
Let say we begin with two chromosomes, A1 and A2.
 We choose a certain crossover point, and then swap the genes, either on the left or right.
We choose a certain crossover point, and then swap the genes, either on the left or right.
The results would look something like this:

We see the introduction of two new chromosomes to the population.
Of course, we are not just limited to one crossover point. We could choose different portions to swap by adding new crossover points,
Mutations
While crossovers can introduce some variety by merging two competitve species, we can further increase the diversity through mutations.
We select can several random bits to modify, or in this example, flip.
It would look something like this:

When to Stop?
There are several ways to determine when to terminate the program.
A common approach is to compare the incremental improvements between generations. If the improvement is small for several generations, we say the algorithm has converged, and we terminate.
Another way is to specify the number of generations beforehand. The program just runs a set number of loops.
Finally, one may terminate when the fitness of a particular chromosome reaches a desired level. This could be useful in some engineering or business applications, where all you need is an answer that is “good enough”.
